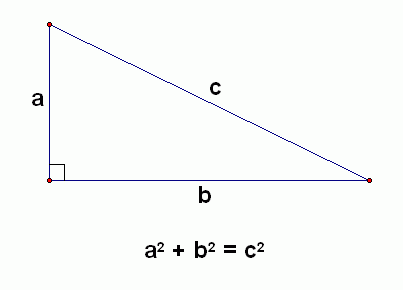This discovery, known as the Pythagorean Theorem states that: The sum of the squares of two of a right triangle is equal to the square of the hypotenuse of that same right triangle. Or in equation form:
a2 + b2 = c2
By using this equation we can find the length of any side of a right triangle provided we have the lengths of the other two sides. For example:
Likewise, this same theorem can be used to find unknown lengths of diagonals and sides in many polygons such as squares and rectangles. See the example below:
This is just one of many ways that the Pythagorean Theorem can be used. How might someone use this mathematical principle in the real world?